Information Criteria
An information criterion is a measure of the quality of a statistical model. It takes into account:
- how well the model fits the data
- the complexity of the model.
Information criteria are used to compare alternative models fitted to the same data set. All else being equal, a model with a lower information criterion is superior to a model with a higher value.
Example
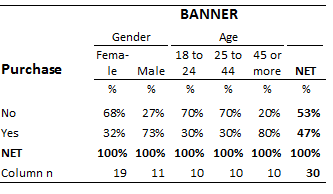
The following table shows the relationship between age and gender and and answer to a survey question ('yes' versus 'no'). This table can be used to construct three models predicting the survey response:
- A gender model (i.e., where gender is used to predict the answer to the 'yes'/'no' question.
- An age model.
- The aggregate model, where it is assumed that there are no segments.
The AICs (defined below) for these models are:
- Gender: 40.59
- Age: 40.44
- Aggregate: 52.98
As the lowest of these values is for age, the information criteria computed suggests that age is the best of the three models.
Common information criteria
Information criteria are computed using the following formula:
where is the Log-Likelihood, is the number of Parameters in the model and is a penalty factor.
AIC
The most widely used information criteria for predictive modeling is Akaike's information criterion,[1], which is usually referred to as the AIC. It employs a penalty factor of 2 and is thus:
BIC
The most widely used information criteria for comparing Latent Class models is the Baysian Information Criterion[2] , which is usually referred to as the BIC. It is computed as:
where is the sample size. Where the sample is size greater than 7 the BIC is a more stringent criterion than the AIC (i.e., all else being equal, it favors simpler models). An intuitive way to think about the difference between the AIC and the BIC is that the AIC is closer to the idea of testing significance at the 0.05 level of significance whereas the BIC is more akin to testing at the 0.001 level (this is just an intuitive explanation; these criteria do not correspond to these p-values).
Relationship to R² and the Adjusted-R²
The R² statistic used to compare regression models is proportional to the Log-Likelihood and thus comparing models using R² is equivalent to selecting them based on the fit to the data without regard to the model complexity (i.e., number of parameters). The Adjusted-R² statistic is similar in its basic goals to an information criteria (i.e., comparing based on fit and number of parameters), but information criteria are generally superior as:
- R² and the Adjusted-R² assume that the Dependent Variable is linear, whereas information criteria can be computed for many types of data.
- The Adjusted-R² is not considered to appropriate penalize model complexity.[3]
Relation to p-values and statistical significance
In the case of the example presented above, an alternative strategy for comparing the models is to compute p-values. For example, with Pearson's Test of Independence, p = 0.04 for the gender model and 0.03 for the age model and thus we obtain the same conclusion as obtained from the AIC. Nevertheless, using the AIC is generally superior as:
- It is not technically valid to use p-values to perform such comparisons.[4]
- The various corrections that have been developed for modifying p-values to permit comparison, such as used in CHAID, [5] are biased [6], and the magnitude of this bias grows the greather the difference between the compexity of the different models (e.g., it makes comparison of, say, predictors with 20 categories versus ones with two categories highly suspect).
References
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ James P. Stevens (2009): Applied Multivariate Statistics for the Social Sciences, Fifth Edition. Routledge Academic.
- ↑ J. K. Lindsey (1999). Some statistical heresies. The Statistician, 48, Part 1, pp. 1-40.
- ↑ Kass, Gordon V.; An Exploratory Technique for Investigating Large Quantities of Categorical Data, Applied Statistics, Vol. 29, No. 2 (1980), pp. 119–127
- ↑ Template:Cite journal